0%

Convolutional Sequence to Sequence Learning

Posted on Edited on

BerlinerMauerFall_ZH-CN1154604596_1920x1080.jpg

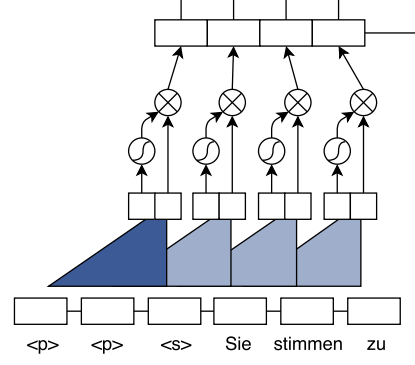
Convolutional Sequence to Sequence Learning 是 Facebook 在 2017 年发表的论文，提出 ConvS2S 模型。Seq2Seq 模型在自然语言处理、计算机视觉、语音识别等领域都有非常广泛的应用。Seq2Seq模型是Encoder-Decoder结构，当应用在 NLP 领域时，它的编码器和解码器通常都都选择 RNN/ LSTM / GRU / SRU 网络。而这篇论文摒弃了RNN网络，而是使用 CNN 来做 Seq2Seq 任务，并且在机器翻译任务上取得了非常不错的结果。

Neural history of NLP

发展

下面我来介绍一下使用神经网路来做 NLP 的发展史：

Seq2Seq + Attention

Seq2Seq

以 Seq2Seq 模型应用到邮件回复系统为例，Encoder 和 Decoder 使用的都是 LSTM。当发送“ Are you free tommorws? ”时，得到自动回复“ Yes, what’s up? ”。首先看 Encoder 部分，在每一时刻 i ，Encoder 接收一个单词，i 时刻隐藏层的计算公式为：
$$
h_i = RNN(h_{i-1},x_i)
$$
直到计算完最后一个单词 ，得到输入的隐藏向量 C 作为 Decoder 的初始状态。Decoder 在 i 时刻的输出的计算公式为：
$$
y_i = RNN(h_{i-1},y_{i-1})
$$
其实 Seq2Seq 模型是比较灵活的，刚刚讲的只是其中一种。还有另一种变体，随机初始化 / 全零初始化 Decoder 的初始状态，然后将编码器得到的隐藏向量 C 和 上一时刻的输出一起输入到解码器中：
$$
y_i = RNN(h_{i-1},y_{i-1},C)
$$

Seq2Seq+Attention

Seq2Seq 模型 Encoder 最终输出向量 C 作为输入句子的特征表示，这里 C 是固定的。当引入 Attention 机制后， C ，Decoder 不同的词对应不同的 C 。

test.jpg

pic

基于RNN的 Seq2Seq + Attention 模型在做什么：

  • Encoder：学习各个词的隐藏表示

  • Attention：根据 Decoder 上一时刻隐藏状态和 Encoder 各个词的隐藏表示计算 Attention 向量

  • Decoder：根据 Decoder 上一时刻隐藏状态和 Attention 向量学习 Decoder 当前时刻的隐藏表示

  • Softmax：生成词分布，获得概率最大值

  • Encoder 学习输入数据中各个词的隐藏表示，并且每个词的隐藏表示包含上下文信息，甚至包含整个输入数据和当前词之间的信息
    $$
    z_i = RNN(z_{i-1}, x_i) \
    $$

  • 当计算 Decoder 第 i 时刻的输出时，Attention 学习 i-1 时刻隐藏状态 / 上下文信息和 Encoder 的各个词的权重
    $$
    a_{ij} = \frac{exp(a(s_{i-1},z_j))}{\sum^{T}{k=1}exp(a(s{i-1},z_k))} \
    C_i = \sum^{T}{j=1}a{ij}s_j
    $$

  • Decoder 根据上一时刻的隐藏表示和当前时刻的 Attention 向量来生成当前词的隐藏表示，并且每个生成词的隐藏表示包含上文信息，甚至包含上文全部信息
    $$
    y_i = RNN(h_{i-1},C_i)
    $$
    最后经过 softmax 层输出生成词

基于RNN的 Seq2Seq + Attention 模型的缺点：

  • 无法并行计算

  • 存在长期依赖问题
    $$
    P(S_{t+1}|S_t) = P(S_{t+1}|S_1,…,S_t)
    $$

  • 不能很好处理句子结构化信息

  • 不平衡

  • 一错到底

  • RNN无法并行计算：RNN网络依赖前一时刻的输出

  • RNN存在长期依赖问题：本质上是马尔科夫决策过程，具有马尔科夫性：
    $$
    P(S_{t+1}|S_t) = P(S_{t+1}|S_1,…,S_t)
    $$
    其中状态 $S_t$ 包含了所有历史相关信息

  • RNN并不能很好的处理句子中的结构化信息：RNN能够很好地学习序列信息，但不能很好地学习词之间的信息、语义信息或者更复杂的信息

  • RNN序列中的第一个元素会进行N次非线性运算，而最后一个元素仅进行1次非线性运算；RNN学习到的隐藏表示是不平衡的，第一个隐藏表示只包含当前词的信息，而最后一个隐藏表示包含所有词的信息

ConvS2S

convs2s.png

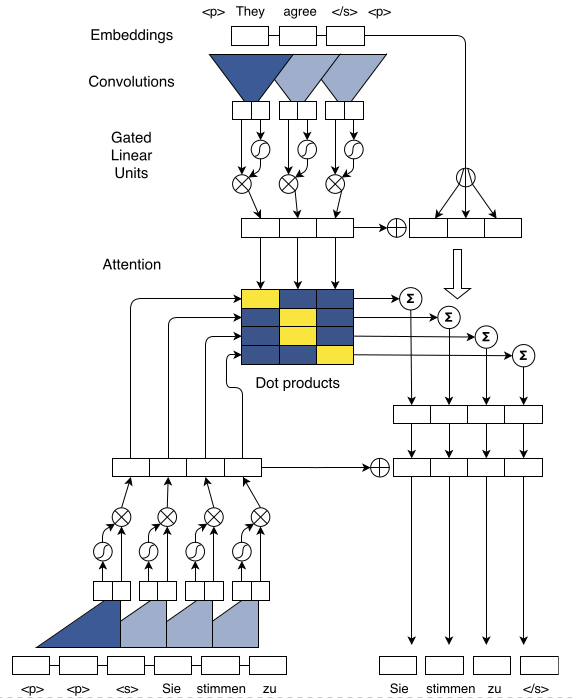
Position Embedding

  1. Data preprocessing

    在 NLP 中数据通常是不定长的，而CNN / RNN 网络要求输入定长数据，所以第一步要做的是数据预处理，将不定长数据转化为定长数据。转化的方法有两种：第一种是填充，第二种是切割，最后得到长度为 m 的输入序列：
    $$
    x = (x_i,…,x_m)
    $$
    得到定长数据之后，需要建立字典，将词和 one-hot 建立映射关系。

  2. Word embedding

    使用Word2Vec、Glove、FastText、WordRank等任意一个 word embedding 模型，将 one-hot 向量转化成连续向量，得 ：
    $$
    w = (w_i,…,w_m), w_i \in R^d
    $$

  3. Position embedding

    对于时间序列来说，尤其是对于NLP中的任务来说，顺序是很重要的信息，它代表着局部甚至是全局的结构，学习不到顺序信息，那么效果将会大打折扣。RNN 擅长处理时序问题，时序问题强调时间的先后顺序，时序问题可以不严格等价于位置问题，先发生的位置在前，后发生的位置在后；CNN 可以使用滑动窗口来捕捉位置信息，只不过在处理时序任务上，CNN 并没有 RNN 那么擅长，所以引入 Position embedding 的目的就是为了让词包含位置信息，从而使 CNN 更好地处理时序任务：
    $$
    p = (p_i,…,p_m), p_i \in R^d
    $$
    Word embedding 是相对于 Word 而言的，Position embedding 是相对于 Position 而言的。什么是位置信息呢？举个例子，“ I love China ”这句话包含3个单词，“I”的位置是1，“love”的位置是2，“China”的位置是3，那么1,2,3就是位置信息。但是直接使用整数来表示位置信息无法应用到神经网络中，通常会将数字映射成 one-hot 向量，比如1映射成(1,0,0)，2映射成(0,1,0)，以此类推。但 one-hot 向量是高维稀疏的，所以通常会将 one-hot 向量转化为类似于 word embedding 的密集连续向量。

    • 一种方式是将 one-hot / 数字输入到 embedding 层得到连续向量
      $$
      \begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0\
      0 & 1 & 0 & 0 & 0 & 0 \end{pmatrix}
      \begin{pmatrix}w_{11} & w_{12} & w_{13}\
      w_{21} & w_{22} & w_{23}\
      w_{31} & w_{32} & w_{33}\
      w_{41} & w_{42} & w_{43}\
      w_{51} & w_{52} & w_{53}\
      w_{61} & w_{62} & w_{63}\end{pmatrix}
      =\begin{pmatrix}w_{11} & w_{12} & w_{13}\
      w_{21} & w_{22} & w_{23}\end{pmatrix}
      $$
      假设句子的长度是6，Position embedding 的维度是3，最终 embedding 层可以得到长度为 m 的句子的 Position embedding。

    • 另一种方式是使用公式计算
      $$
      PE_{\left ( pos,2i \right )}=sin\left ( \frac{pos}{1000^{2i/d}} \right ) \
      PE_{\left ( pos,2i+1 \right )}=cos\left ( \frac{pos}{1000^{2i/d}} \right )
      $$
      其中，pos表示位置，i 表示维度，d 表示 Position Embedding 的维度。生成位置向量中偶数部分的值使用第一个公式，生成位置向量中奇数部分的值使用第二个公式。

      比如英语句子“Tom chase jerry”，我们想把 Tom 映射为3维的位置向量，那么pos=1,d=3，而位置向量的每个值为：
      $$
      PE_{\left ( 1,0 \right )}=sin\left ( \frac{1}{1000^{0/3}} \right )
      $$

      $$
      PE_{\left ( 1,1 \right )}=cos\left ( \frac{1}{1000^{0/3}} \right )
      $$

      $$
      PE_{\left ( 1,2 \right )}=sin\left ( \frac{1}{1000^{2/3}} \right )
      $$

      Position Embedding本身是一个绝对位置的信息，但在语言中相对位置也很重要，Google选择前述的位置向量公式的一个重要原因是：
      $$
      sin(α+β)=sinαcosβ+cosαsinβ \
      cos(α+β)=cosαcosβ−sinαsinβ
      $$
      这表明位置 p+k 的向量可以表示成位置 p 的向量的线性变换，这提供了表达相对位置信息的可能性。

  4. Element represention

    结合位置向量和词向量有几个可选方案，可以把它们拼接起来作为一个新向量，也可以把位置向量定义为跟词向量一样大小，然后两者加起来。Facebook 选择的是前者：
    $$
    e=(w_1+p_1,…,w_m+p_m),e_i \in R^d
    $$

同理，对解码器的输入也使用 Word embedding + Position embedding ，得：
$$
g = (g_1,…,g_n)
$$
下图是在 WMT’14 English-German 数据集上做的实验，PPL表示困惑度，越小越好；BLEU越大越好。从表中可以看出，加入 Position embedding 之后，可以或多或少的提高模型的效果。即使不加 Position embedding ，ConvS2S 模型也能取得不错的效果，原因是 CNN 网络本身就能利用位置信息。

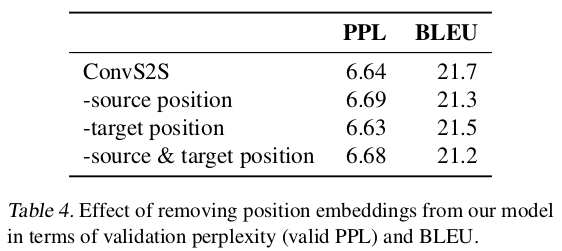
convtable4.png

Convolutional Block Structure

Encoder 第 l block 的输出为：
$$
z^l = (z_1^l,…,z_m^l)
$$
Decoder 第 l block 的输出为：
$$
h_l = (h_1^l,…,h_n^l)
$$

  1. Gated Convolutional Networks

    Language Modeling with Gated Convolutional Networks

    门卷积借鉴了LSTM中门的思想，首先回顾一下LSTM

    pic
    $$
    f_t = \sigma (W_f \cdot [h_{t-1},x_t] + b_f) \
    i_t = \sigma (W_i \cdot [h_{t-1},x_t] + b_i) \
    \tilde{C}t = tanh(W_C \cdot [h{t-1},x_t] + b_C) \
    C_t = f_t \otimes C_{t-1} + i_t \otimes \tilde{C}t \
    o_t = \sigma (W_o \cdot [h    {t-1},x_t] + b_o) \
    h_t = o_t \otimes tanh(C_t)
    $$

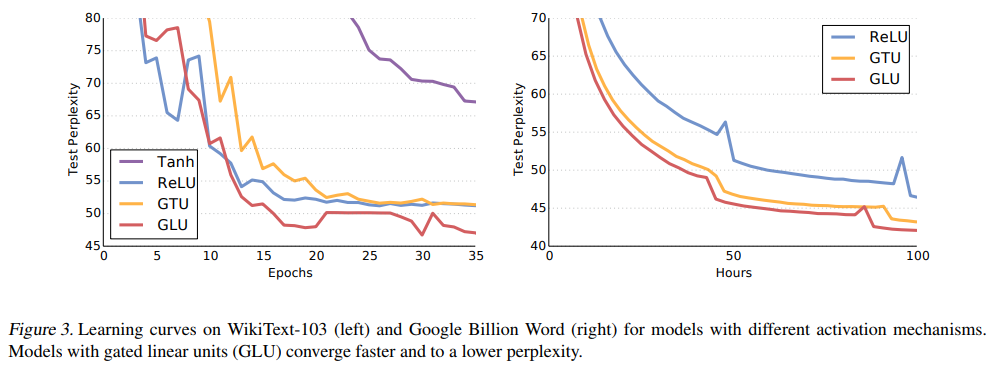
    实际上 LSTM 通过 sigmoid 函数学习概率，来决定哪些数据应该以多大比例遗忘，哪些数据应该以多大比例记住。门 CNN 同理，通过 sigmoid 函数来决定当前的特征应该以多大比例保留：

    $$
    h^l(X) = (X * W + b) \otimes \sigma (X * V + c) \
    or \quad h^l(X) = tanh(X * W + b) \otimes \sigma (X * V + c) \
    $$
    第一种叫Gated linear unit (GLU) ，第二种叫 Gated tanh unit (GTU)

    GLU的优点：

    • 按一定比例保留数据

    • 具有拟合非线性函数能力的同时保留线性路径，减缓梯度消失问题
      $$
      \bigtriangledown [X \otimes \sigma(X)] = \bigtriangledown X \otimes \sigma(X) + X \otimes \sigma(X)^{‘} \bigtriangledown X
      $$

      接下来介绍如何利用一维卷积和GLU来获得隐藏表示$h^l_i \in R^d$ ：

      convblock.png

      1
      2
      3
      4
      5
      6
      7
      8
      # method 1
      z = keras.layers.Conv1D(2d, 3, padding='same',activation=None)(e)
      z = z[:,:,:d] * K.sigmoid(z[:,:,d:])

      # method 2
      z1 = keras.layers.Conv1D(d, 3, padding='same',activation=None)(e)
      z2 = keras.layers.Conv1D(d, 3, padding='same',activation='sigmoid')(e)
      z = z1 * z2

      Encoder 可以获取全部数据信息，所以计算每个词的隐藏表示时可以利用上下文信息甚至利用整句话的信息。但是对于序列生成任务来说，Decoder 的每个词是逐个生成的。由于是监督任务，在训练时可以得到 Decoder 的全部输入。但是在测试时我们并不知道 Decoder 的后续词。所以在 Decoder 部分我们需要对卷积做一些改变，让它只利用上文信息，而无法利用下文信息。具体的做法是给卷积核加 mask 掩码：
      $$
      h^l(X) = (X * (W \otimes I) + b) \otimes \sigma (X * (V \otimes I) + c)
      $$
      其中，$I$ 表示掩码矩阵。举个例子，词嵌入的维度是4，一维卷积核大小是5，它的掩码矩阵是：
      $$
      \begin{pmatrix}w_{11} & w_{12} & w_{13} & w_{14}\
      w_{21} & w_{22} & w_{23} & w_{24}\
      w_{31} & w_{32} & w_{33} & w_{34}\
      w_{41} & w_{42} & w_{43} & w_{44}\
      w_{51} & w_{52} & w_{53} & w_{54}\end{pmatrix}
      \otimes
      \begin{pmatrix}1 & 1 & 1 & 1\
      1 & 1 & 1 & 1\
      1 & 1 & 1 & 1\
      0 & 0 & 0 & 0\
      0 & 0 & 0 & 0\end{pmatrix}
      $$
      pic

      pic

  2. Residual block

    Deep Residual Learning for Image Recognition

    $$
    h_i^l = h_i^l + h_{i-1}^l \
    or \quad h_i^l = f(h_i^l) + h_{i-1}^l \
    or \quad h_i^l = h_i^l + f(h_{i-1}^l) \
    or \quad h_i^l = f(h_i^l) + f(h_{i-1}^l) \
    or \quad h_i^l = f(h_i^l + h_{i-1}^l)
    $$

    优点：

    • 减缓梯度消失

      pic

      深层网络比浅层网络更具表现力，但随着网络加深，模型越来越难以训练，存在梯度消失问题。如上图加入残差块后，进行反向传播时，$a^{[l+2]}$ 层的梯度会有两个传播路径：沿着深层网络传播；沿着跳跃连接传播。即使深层网络反向传播过程中梯度为0，但是由于存在跳跃连接提供梯度，所以会减缓梯度消失的问题。

    • 保证网络性能
      pic

  3. add layers

    • 捕获更多的上下文信息

      pic

    • 理论上，深层网络比浅层网络更具表现力

      pic

Multi-step Attention

  1. Attention

    Attention 机制从大量信息中有选择地筛选出少量重要信息并聚焦到这些重要信息上，忽略大多不重要的信息。

    pic

    上图中，key 和 value 表示原语句 source 的元素；query 表示目标语句 target 的元素。Attention 机制可以分为3个阶段。以机器翻译为例，key 和 value 都表示原语句的特征表示，qyery 表示上一时刻的隐藏状态 / 上文特征。公式如下：

    • 计算 query 和 key 的相似度
      $$
      Similarity(Query,Key_i) = Query\cdot Key_i
      $$

    • softmax 归一化得到 key 对应 value 的权重
      $$
      a_i = Softmax(Similarity_i)=\frac{e^{Similarity_i}}{\sum_{i=1}^{L_x}e^{Similarity_i}}
      $$

    • 对 value 进行加权求和
      $$
      Attention(Query,Source)=\sum_{i=1}^{L_x}a_i\cdot Value_i
      $$

  2. Multi-step Attention
    $$
    d_i^l = W_d^l h_i^l + b_d^l + g_i \
    a_{ij}^l = \frac{exp(d_i^l \cdot z_j^u)}{\sum_{t=1}^{m}exp(d_i^l \cdot z_t^u)} \
    c_i^l = \sum_{j=1}^{m} a_{ij}^l(z_j^u + e_j)
    $$

    • 第一个公式：残差，将 Decoder 第 $l$ 层的隐藏表示进行线性变换，然后与 Decoder 的输入 $g$ 相加作为第 $l$ 层最后的隐藏状态
    • 第二个公式：$z_j^u$ 表示 Encoder 最后一层的输出的第 $j$ 个隐藏表示；计算 Encoder 各个隐藏表示与 Decoder 的隐藏特征表示 $d_i^l$ 的相似度，再进行 softmax 归一化
    • 第三个公式：对 value 进行加权求和，此时 query 是Decoder 第 $l$ 层的第 $i$时刻的特征 $d_i^l$；key 是Encoder 最后一层的输出 $z_j^u$； value 是 $z_j^u + e_j$ 。为什么 value 要加入 $e_j$ 信息？ $z_j^u$ 表示 $j$ 时刻词的特征表示，这个特征表示包含上下文信息；$e_i$ 提供对应输入元素的词信息。在机器翻译这种序列任务中存在词与词对齐的要求，以前的对齐方式是逐元素对齐，这也印证了加入特定输入元素的点信息是有好处的。局部 Attention 的一种对齐方式就是选择对应位置元素，并且 key-value 记忆网络也印证了这一点。

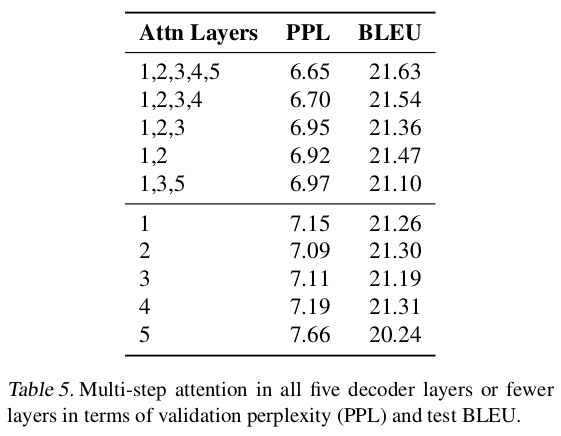
convtable5.png

Experiments

  • 一般建立字典方式：使用<UNK>表示集外词
  • 双字节编码（byte-pair encoding, BPE）：把罕见词拆分成“子词单元”的组合，解决集外词和罕见词问题
  • Word pieces：把单词分别为单词块，解决集外词和罕见词问题

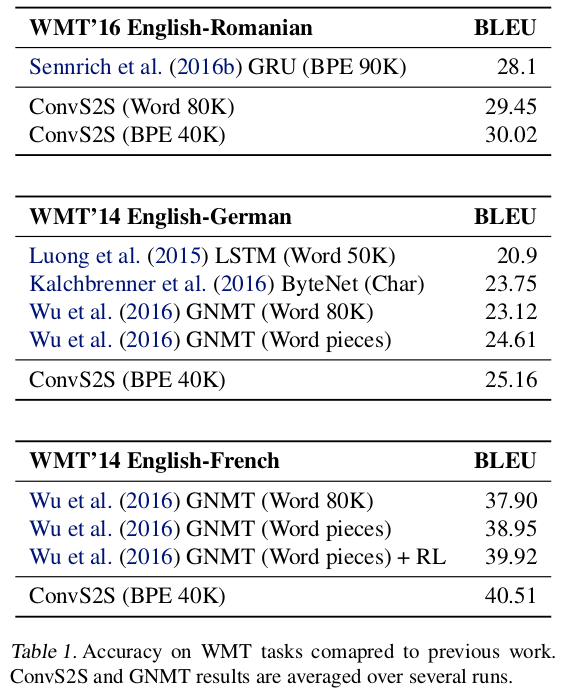
couvs2stable1.png

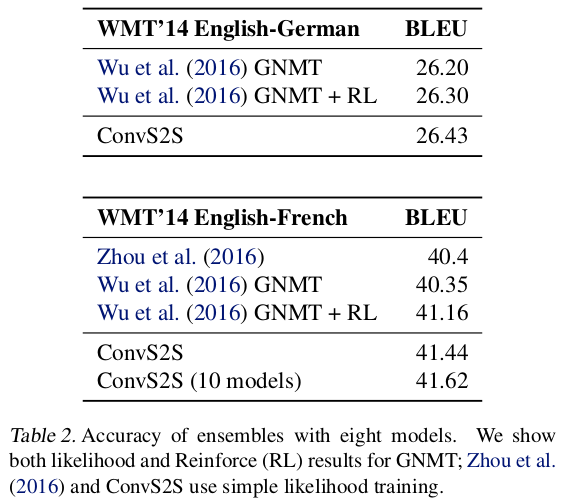
convs2stable2.png

convtable3.png

  • 贪心搜素（greedy search）

    生成第一个词的分布以后，选择最有可能的第一个词，然后根据第一个词继续挑选出最有可能的第二个词，以此类推，这种算法就叫做贪心搜索。但是真正需要的是挑选出一个序列，使得 $y^1,…,y^n$ 的概率最大化，而贪心搜索不能满足这种需求。

    1
    2
    3
    4
    French: Jane visite l'Afrique en septembre

    Jane is visiting Africa in September
    Jane is going to be visiting Africa in September

  • 集束搜索（beam search）

    每一时刻我们都会得到每个词的概率，如果想使得 $y^1,…,y^n$ 的概率最大化，最笨拙的想法是保留所有词的概率值，最后从 $size^{n}$ 个序列中选择概率最大的作为最终的输出序列，但是这种方式的计算成本是无法接受的。集束搜索的方式是每次选择前 d 个概率最大的词。

    pic